Conteúdos
– Sequências numéricas
Objetivos
– Compreender os números de Fibonacci e sua origem
– Identificar números de Fibonacci na natureza
– Completar uma sequência de Fibonacci
– Criar um retângulo e uma espiral de Fibonacci
1ª Etapa: Início de conversa
Os números de Fibonacci são uma ideia matemática muito rica e que pode ser apresentada de diversas maneiras na sala de aula. No entanto, normalmente, não ocupam muito espaço no currículo escolar e, muitas vezes, são apresentadas apenas como um exemplo no tópico que aborda as sequências numéricas.
O objetivo desse plano de aula é apresentar aos estudantes os números de Fibonacci e, por meio de uma atividade prática, identificar a presença desses números na natureza.
Reconhecer padrões matemáticos na natureza de forma prática é uma maneira eficaz de estimular os estudantes a conectarem a Matemática com o mundo que nos cerca. Além disso, a experiência é uma ótima oportunidade para (re)conhecer frutas e legumes diversos.
2ª Etapa: Motivação dos estudantes
Inicie a aula expondo a fotografia de uma margarida. Escolha uma em que seja possível contar com facilidade a quantidade de pétalas e observar os espirais do miolo. Pergunte aos estudantes se alguém sabe o nome da flor, depois, escreva-o no quadro. Volte a atenção para a fotografia e solicite aos estudantes que observem as formas e as quantidades.

Fonte da imagem. Acesso em 11 Agosto 2018.

Fonte da imagem. Acesso em: 11 Agosto 2018.
– Quantas pétalas ela tem?
– Qual o formato do miolo? O que é possível observar sobre o miolo?
Destaque as espirais no miolo e peça que os estudantes tomem nota das observações e da quantidade de pétalas.
Parta para uma nova fotografia, dessa vez abra a fotografia de uma pinha. Escolha uma em que seja possível observar e contar a quantidade de espirais formados na superfície da pinha. Pergunte aos estudantes se alguém sabe o nome e acrescente a informação de que as pinhas que estamos acostumados a ver, na verdade, são flores. Escreva o nome da flor no quadro. Volte a atenção para a fotografia e solicite aos estudantes que observem os espirais formados na superfície da pinha.

Fonte da imagem. Acesso em: 11 Agosto 2018.
– Os espirais estão apenas em uma direção?
– Quantos há em cada direção?
Solicite aos estudantes que tomem nota das observações identificando a quantidade de espirais no sentido horário e a quantidade de espirais no sentido anti-horário.
Para encerrar a etapa motivadora, questione se é possível observar alguma semelhança entre essas flores tão distintas. Aproveite para estimular reflexões sobre os espirais e as quantidades de pétalas da margarida. Algumas perguntas podem ser interessantes:
– Será que todas as margaridas têm a mesma quantidade de pétalas?
– Será que a quantidade de espirais da margarida é a mesma que a quantidade de espirais da pinha?
– Será que toda pinha tem a mesma quantidade de espirais para cada lado?
3ª Etapa: Os números de Fibonacci
Nessa etapa, propõe-se uma abordagem mais teórica. Exponha o conteúdo utilizando a lousa e dialogando com o grupo para manter os estudantes focados.
Para compreender melhor o que essas flores têm em comum, é necessário entender um pouco sobre um livro escrito há mais ou menos 800 anos por um Matemático chamado Leonardo de Pisa, mais conhecido como Fibonacci. Quando escreveu o livro (chamado “Liber abbaci”), Fibonacci incluiu um problema mais ou menos assim:
Um homem coloca um par de coelhos num cercado. Quantos pares de coelhos serão produzidos deste par em um ano, considerando que, a cada mês, um par de coelhos produz um novo par que começa a ficar produtivo a partir do segundo mês de nascimento?
Para solucionar esse problema, Fibonacci encontrou a seguinte sequência de números:
0,1,1,2,3,5,8,13,21,34,55,89,144…
Esses números descrevem a situação dos coelhos e ficaram conhecidos como números de Fibonacci.
Solicite aos estudantes que tentem descobrir como encontrar números de Fibonacci. Revele que, para obter o próximo número da sequência, é necessário somar os dois termos anteriores e exemplifique o processo.
Explique que essa construção só é possível partindo dos elementos 0 e 1 como primeiro e segundo elementos da sequência.
Para ilustrar como a sequência pode ser representada geometricamente, construa uma espiral de Fibonacci utilizando quadradinhos coloridos na lousa. Questione como essa teoria se relaciona com as fotos observadas no início da aula. Espera-se que os estudantes relacionem a construção da espiral com as fotografias observadas, no entanto, estimule uma reflexão sobre como os números de Fibonacci poderiam ser apresentados naquele contexto.
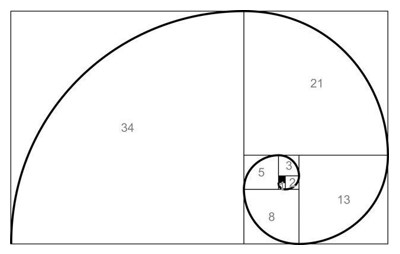
Fonte da imagem. Acesso em: 11 Agosto 2018.
4ª Etapa: Observação das frutas e legumes
Agora que os estudantes já reconhecem a sequência de Fibonacci, será o momento de tentar encontrar esses números nas frutas e legumes que eles trouxeram para essa aula. Prepare uma faca e fique responsável pelo corte das frutas e legumes. Não autorize que os estudantes utilizem a faca. Dependendo da fruta ou legume, é recomendável cortar de uma forma que dê para observar os padrões que revelem os números de Fibonacci. Veja alguns exemplos de cortes nas imagens a baixo. Há três fatias de banana e, abaixo, uma fatia de maçã. Observe que as bananas apresentam três seções e as maçãs apresentam 5 seções. O número 3 e o número 5 são números de Fibonacci.


As laranjas podem ser cortadas de forma que seja possível observar a quantidade de gomos. A chance de os gomos serem um número de Fibonacci é grande. No caso do abacaxi, observe os espirais formados pelos espinhos da casca. A quantidade de espirais em cada sentido deve ser um número de Fibonacci. Utilizar fitas adesivas, de cores distintas, para identificar os espirais do abacaxi pode facilitar o trabalho. No caso dos brócolis e da couve flor, é possível observar os espirais em suas superfícies com algum cuidado. No caso de outras frutas e legumes, pode ser interessante investigar se é possível localizar algum número de Fibonacci ou espiral.
Pode ser que em alguns casos seja difícil ou impossível encontrar um padrão de Fibonacci. Isso também caracteriza uma descoberta e um aprendizado, pois nem tudo na natureza segue as regras dessa sequência. Existem vários tipos de sequências. Espera-se que a maior parte dos itens trazidos pelos estudantes revele, de alguma forma, um número ou espiral de Fibonacci.
Peça aos estudantes que fotografem suas descobertas para a montagem de um cartaz, destacando as informações observadas com uma fotografia. Os cartazes podem ser expostos nas paredes da sala de aula ou em varais.
Materiais Relacionados
1 – Você poderá encontrar motivações para abordar sequências de Fibonacci, em sala de aula, no artigo “O que é a sequência de Fibonacci?” da revista Superinteressante.
2 – Caso seja possível, pesquise por “frutas Fibonacci” no site Google Imagens e, uma semana antes dessas aulas, de acordo com seu planejamento, combine com os estudantes para que tragam frutas e legumes diversos para a sala de aula. Solicite à escola, se possível, lupas e facas para analisar e cortar as frutas e legumes trazidos.
3 – Você poderá preparar a exibição do vídeo “Fibonacci Sequence in Nature”. Para isso, será necessário que faça pausas para explicar aos estudantes onde encontrar números de Fibonacci nas imagens apresentadas.
4 – Nesse plano de aula, por diversas vezes, será interessante exibir aos estudantes fotografias encontradas na Internet. É importante selecionar essas fotografias com antecedência. Todas as fotografias indicadas aqui podem ser encontradas no site Google Imagens, procurando por “***** fibonacci”, onde “*****” deverá ser substituído por aquilo que procura. Por exemplo, para essa aula será necessário buscar a fotografia de uma pinha, para isso, busque “pinha fibonacci” na ferramenta de busca indicada.


Muito interessante esse plano de aula, com certeza farei uso ao introduzir os números de Fibonacci